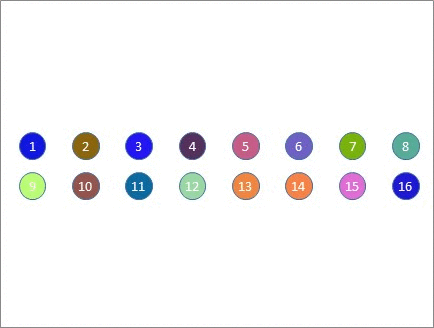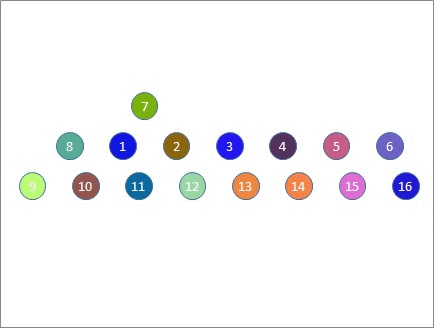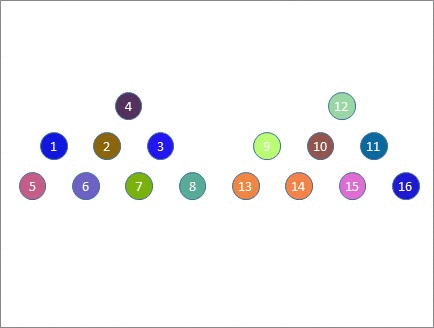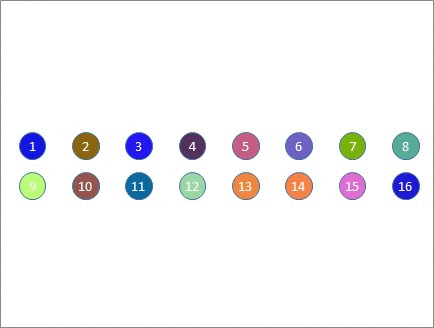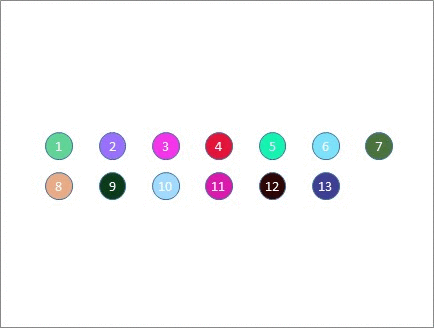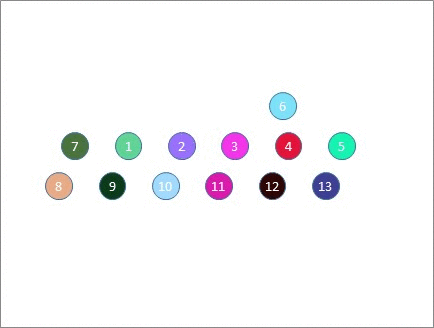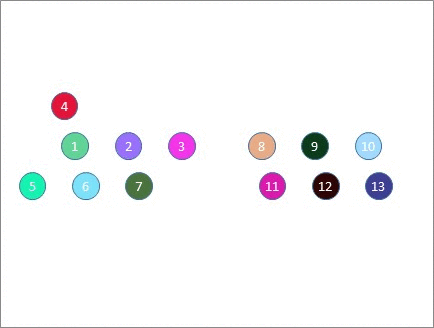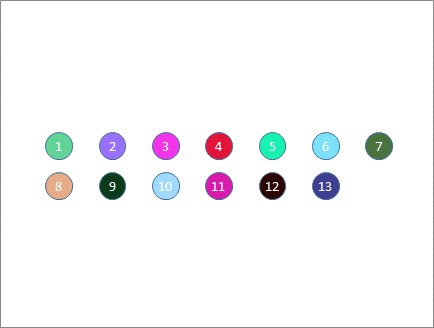Business Networking

Maths and Speed-Networking (Part 1)

Kevin Pretorius Business Networking 07 March 2023

Speed networking (loosely based on speed?_dating_) is an increasingly popular way to organize business networking events. Participants sit at tables in twos, threes or larger groups, and talk about their businesses in turn for 60 seconds. When everyone at the table has had the chance to speak, participants move to new tables (according to some predetermined plan or rule) whereupon they repeat their pitch in front of a new group of eager listeners.

In principle, this is a very efficient way of getting to meet most of the people in the room. It forces everyone to be succinct about what they say about their business?and allows everyone to quickly identify people they'd like to spend more time with afterward. The?_problem_?is that organizing how people should best move between tables in order to meet the maximum number of people (whilst avoiding meeting people they've met before) isn't easy to get right?and requires a little forethought and mathematical insight.

In practice, I've yet to attend a speed networking meeting which gets this right (at least not for groups of three or more). So here's my analysis of what goes wrong, and how to organize this without hitting these issues.

---

What Goes Wrong (and why)?

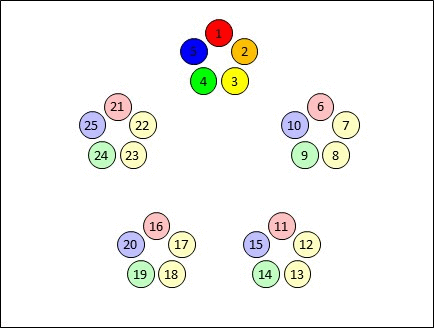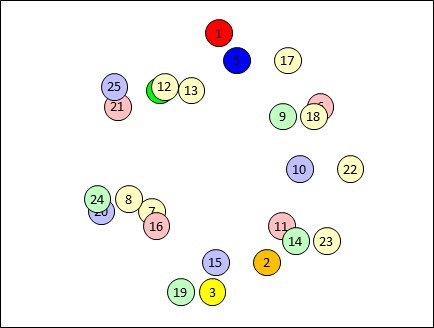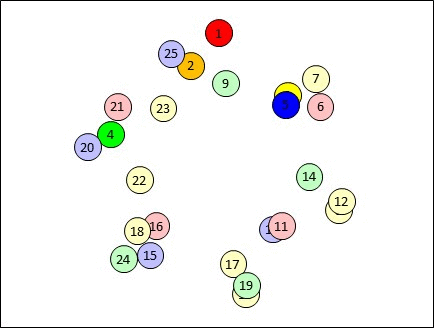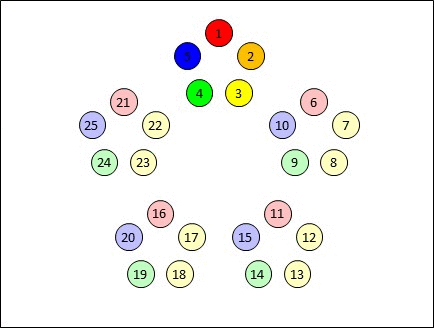
Consider the following example, with 18 participants sitting at 6 tables of 3, which is exactly the situation I encountered at a speed networking event earlier this year. Each person at each table was assigned to a group (here illustrated as red, green and blue) and after everyone at the table had spoken, the greens moved clockwise one table, the blues moved anti-clockwise one table, and the reds?remained seated.

I've produced this simple gif to illustrate the idea, using saturated colours to highlight the positions of those who started out at the top table so you can follow their movement.

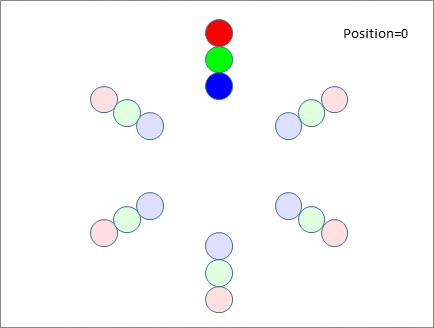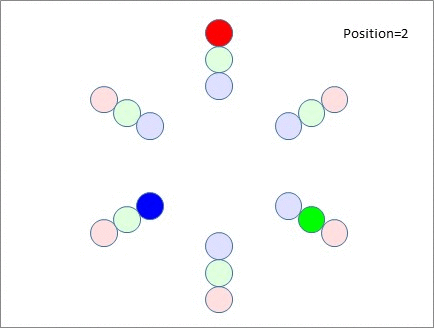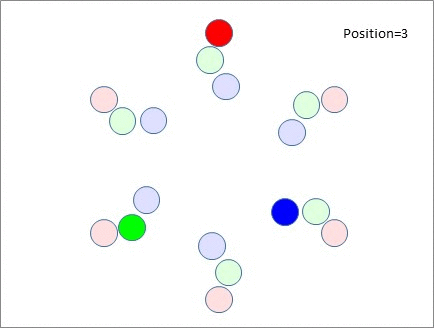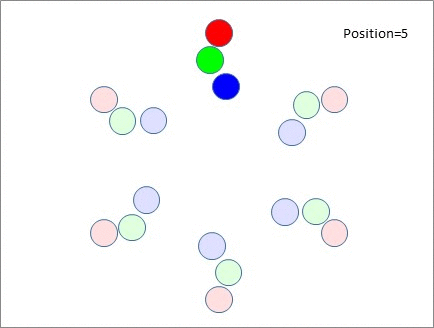
You'll notice that after 3 moves, our green and blue participants (who were initially at the top table) meet each other again on the far side - which is obviously undesirable. There's no point delivering your elevator pitch to someone who heard it just 10 minutes ago. Also note that this issue isn't restricted to just the top table. After that 3rd move, EVERY green or blue participant is experiencing the same issue. You can almost hear "Hello again!" being voiced at every table after that 3rd move. And it's not unique to the 3rd position - After the 4th and 5th moves, the green and blue participants meet up with the blue and green participants they met 3 moves earlier. Only the red participants keep meeting new people!

The Apparent Problem

If you look at the diagram, the reason is very easy to see - it's because the blue and the green participants are moving away from each other at a rate of two tables per move. Which means after 3 moves they are back together because 2 x 3 = 6 tables.

So could you choose different rates of separation and avoid this problem? Sadly the answer is no. If you keep red and green moving as they are but move blue 2 tables anti-clockwise at each turn, then now blue meets green after just 2 turns (which is worse), and blue meets red after 3 turns (which just rubs salt into the wound). You can work through as many combinations as you like, but you can't arrange for the red, green and blue to?move in simple patterns like this without at least one pair of them moving?2 or 3 tables apart (or towards each other) per step, leading to them meeting up again in 2 or 3 moves, or (vacuously) every move.

The Fundamental Problem

The fundamental problem here is the number of tables. 6 has too many?_factors_?- numbers (like 2 and 3) which divide into 6 without a remainder. The only available solution works by (say) one person remaining seated, whilst a second person moves 1 table a time. If you try to move that second person 2 or 3 tables at a time you'll run into trouble (as we've seen above), and bear in mind that moving 4 (or 5) tables at a time is the same as moving 2 (or 1) tables at a time in the opposite direction. There is NO solution for how to add a third person to this arrangement which doesn't duplicate encounters.

The Easy Solution

The answer lies with prime numbers - numbers like 5, 7 or 11 which are only divisible by themselves and 1. If you want an easy life when organizing speed networking with groups - always have a prime number of tables.

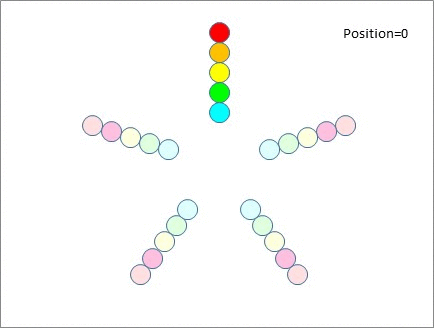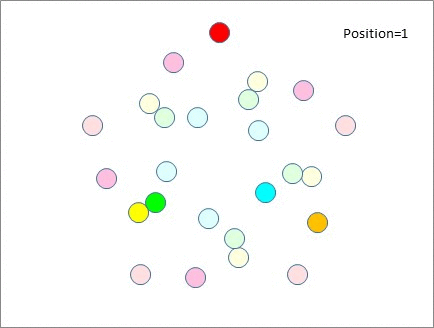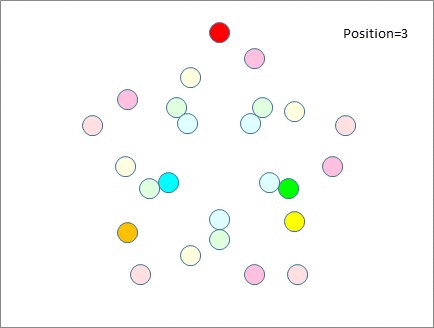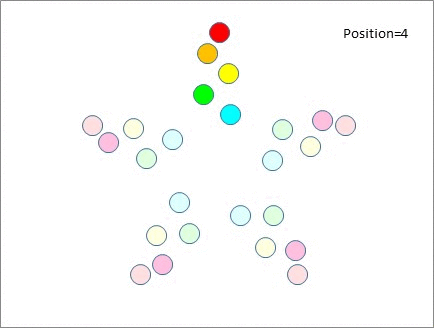
Let's take 5 tables as an example. Now you can have up to 5 people per table and no-one will meet twice if you move them between tables as follows:

- One person remains seated (red),
- One person moves clockwise one table at a time (orange) and one person moves anti-clockwise one table at a time (yellow)
- One person moves clockwise TWO tables at a time (green) and one person moves anti-clockwise TWO tables at a time (cyan).

Here's how that looks. Note that no-one from the top table meets anyone from the top table again until?the end of the session. This is also true for everyone else. All participants meet fresh people after every move.

So we've accommodated 5 people on each of 5 tables without messing up, whereas with 6 tables we couldn't accommodate more than 2 people per table.

And if you still remain to be convinced, here are 7 tables, shuffling up 7 people at a time, by moving them 0, 1, 2 and 3 places clockwise and anti-clockwise at a time.

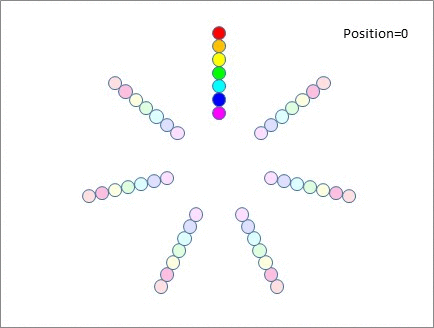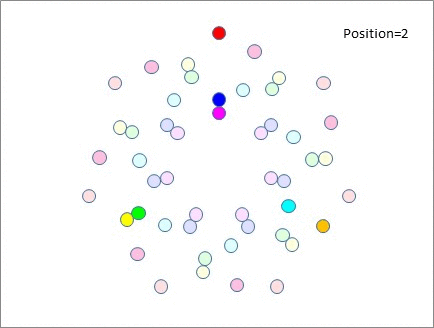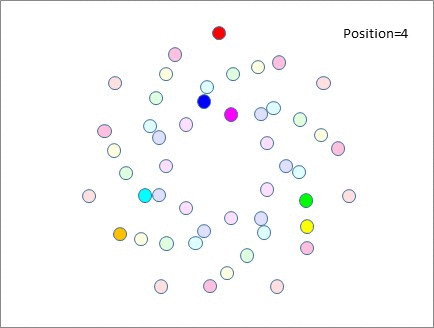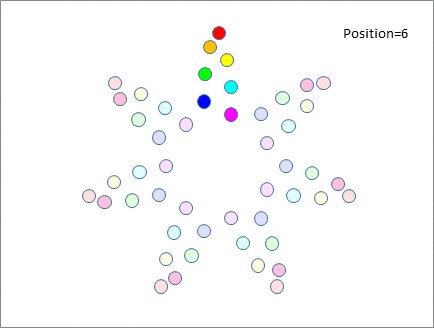
So the moral of this story is that if you're intending to organize a speed networking event as per the method above, then?**pick a prime number of tables**, and you'll be fine. For 10..25 participants use 5 tables, and up to 5 participants per table. From 26..49 participants use 7 tables and up to 7 participants per table. If you've from 50..121 participants, you can use 11 tables and up to 11 participants per table, but you'll probably want to issue tickets to tell people which table they need to be on, as the chances of everyone correctly moving 2 (or more) tables at a time without them miscounting or getting lost is possibly quite small! If you've less than 10 people, you?_could_?organize an event with 3 tables of up to 3 people, but why would you?

Kevin Pretorius, Excel Wizardry

Footnote: These animated GIFs were assembled from individual frames using the free Animated GIF Maker at?[http://gifcreator.me/](http://gifcreator.me/). The individual frames were generated with Excel software written specifically for these blog articles.

Maths and Speed-Networking (Part 2)

Kevin Pretorius Business Networking 07 March 2023

In my previous blog, I wrote about how to organize a speed networking event for large groups using simple rules and prime numbers. This applies to networking events which are organized around tables. Another popular model, and one closer to the idea of speed dating, is to set up two rows of chairs facing each other, and to have people speak one on one for 60 seconds at a time, before moving on to the next encounter. A bit like this...

This works perfectly well of course, except that you only get to meet half the people in the room - which is possibly OK if you're speed dating, but less satisfactory when your goal is to meet as many of the participants as possible. So after you've met everyone on the opposite facing chairs - what do you do next?

This is a situation which arose at a meeting I attended a couple of years ago. There was plenty of time available, people realised?that they'd only met half the attendees, but the organizer didn't quite know how to proceed, and what actually followed simply didn't work.

For future reference - a perfectly reasonable solution is as follows.

The first thing to realise, is that in the above diagram, everyone in the top row has met everyone in the bottom row, but no-one else in the top row. And the same is true for everyone in the bottom row. So why not separate the two rows, and organize two parallel speed-networking events - one for the people in the top row, ?and one for people in the bottom row. And when THOSE speed networking meetings have completed, repeat the process again, and organize four parallel speed-networking events for the remainder. For 16 participants, one final 4th set of 8?meetings will ensure everyone has met everyone, but I won't object if you stop before then.

Here's an animation of exactly this process for 16 participants...

Admittedly, you don't get convenient powers of two very often, so what are you to do when you have to deal with odd numbers? It's really not much more complicated. It just means that you set out an empty chair (to make up the even number), and have a person who takes a rest - or talks to the empty chair if they prefer. Everyone will do that at some point. Here's an example with 13 people, which runs into odd numbers all the time...

So the next time you find yourself wondering how to shuffle people up after a first round of speed networking - split them in two!

Footnote: These animated GIFs were assembled from individual frames using the free Animated GIF Maker at (http://gifcreator.me/). The individual frames were generated with Excel software written specifically for these blog articles.

Maths and Speed-Networking (Part 3)

Kevin Pretorius Business Networking 07 March 2023

In my previous 2 blogs I discussed how to organize Table-based speed networking using prime numbers, and 1:1-based networking using repeated binary sub-division. OK I didn't use those exact terms, but that is indeed what I did.

It occurs to me that for Table-based networking, there's one extra step we can do, to ensure that everyone meets everyone else, and it's illustrated below...

---

To recap, this diagram shows 25 people meeting in 5 groups (or tables) of 5. We assign a colour to each person at the table, and we provide instructions on how each colour moves between tables once all the people at the table have introduced themselves to one another. Reds stay where they are, oranges move one table clockwise, yellows move one table anticlockwise, greens move two tables clockwise, and blues move two tables anti-clockwise.

This scheme ensures that everyone in each colour group meets everyone in each of the other colour groups.

I've used stronger colours for the people who start out at the top table, to make it easier to follow where they go.

But there's one addition to the scheme described in part 1 of this blog, and that's to deal with the problem that no reds have met any other reds, no oranges have met any other oranges, etc.

How did we solve this? Well very, very easily. We've just added one final step where we gather all of the reds onto the first table, all of the oranges to the 2nd table, all the yellows to the third table, etc and we hold one last round of introductions. Then everyone has met everyone else!

Footnote: These animated GIFs were assembled from individual frames using the free Animated GIF Maker at http://gifcreator.me/. The individual frames were generated with Excel software written specifically for these blog articles.