In my previous blog, I outlined an approach whereby Excel could provide much interactive support to help break simple substitution ciphers - by counting letter frequencies, by applying guesses, and by highlighting popular bigram, trigram and quadgram patterns and frequencies in your coded message.
But it was still a considerable challenge and a chore, which prompts the question - Can this be solved automatically? Is there some way you can just press a button and have the computer figure out what the plaintext message actually says....?
Let's say this is the message that I'm trying to crack...
Usually, when I have something I want to automate, I work through a few examples, trying to understand my own manual approach well enough that I can abstract some algorithms for solving the problem. But in this case, that didn't seem to help. For sure - I'd start with some guesses about popular letters, I'd look for possible short words in the plain text message, and I'd look at some of those bigram and trigram frequencies - both for feedback about the likelihood that I was on the right track and/or to suggest statistically likely things to try. At some point I would get a gut feeling that I was not on the right track, unwind what I'd done and try something else.
But it was all a bit random and intuitive - not a definite procedure.
How about if I forced myself to be procedural - maybe trying all possible combinations until something works?
Unfortunately, that's completely unrealistic - as there are more than 403 million, million, million, million combinations to try, and then how would I know if something had worked? The computer doesn't understand English and wouldn't be able to tell whether the deciphered text made sense, nor could it develop a gut feeling for whether something was going well.
A common approach to tackling the problem of finding solutions in huge search spaces, is to try to find a way to focus on the most promising-looking options and to ignore the rest. We do this unconsciously all the time - you don't (for example) plan a driving route from A to B by considering driving 100 miles in the wrong direction first, just as much as you wouldn't start solving a cipher by asking - which letter corresponds to q?
So let's start by making a list of all 26 possible guesses for the most popular letter in the cipher (ie. G in this case) and try to assign some score to each in turn, to measure in how good each guess is.
Clearly the letter frequency tables can come to our aid here. We can score our choices by simply comparing the frequency of our chosen letter in the plain text, with what we would expect for normal English. So here we have guessed G = e, and we can see that these letters have a reassuring similarity in their frequency of occurrence.
But we need to score this somehow. I chose to use the absolute difference of these frequencies divided by their sum, which produces a score close to 0 if the numbers are similar, and close to 1 if they are very different. In the example message with G being the most popular letter in the cipher (at 13.3%) guessing the most popular letter in Enqlish e (at 12.5%) produces a score of abs(13.3 - 12.5)/(13.3+12.5) = 0.031 - for that letter alone.
There are 22 separate letters appearing in the above cipher (ie 4 letters are not used). As the other 21 letters in the cipher are not yet assigned a guess, they have a 0% chance of occurring in English, which gives them a score of 1.0. Consider for example the letter I in the cipher which occurs 9.0% of the time, but isn't yet assigned a guess. This has a score of (9-0)/(9+0) which is exactly 1.0.
This is true for all the 21 unassigned letters, so the overall score we would give the entire decryption key at this point is 21+0.031. For normalisation purposes I divide this by the score we would get if no letters were assigned at all (i.e. 22.0) to give 21.031 / 22.0 = 0.956.
So now I have some measure of how good each of the first letter guesses are. The next step is to make the assumption that the correct answer is somewhere in the top 10 scoring letters (remembering that a low score is a good score). So I discard the rest, leaving just the following...
Now I work through each of these entries in the list and create 250 two letter-entries by adding all possible guesses for the second most common letter. I then work through each of these, scoring them, sorting them, and deleting all except the top 10, leaving a result like this one below...
If we continue in this way until the final letter, we might hope to end up with a best-possible decryption key (so long as we didn't accidentally discard it by selecting only the Top 10). And the search is tractable, because our approach ensures that we examine no more than 250 potential decryption keys at each step.
However, and it may be obvious to you already, this process will inevitably pick letters in the order e,t,a,o,i,n because that's the order they appear in Engish letter frequency tables - which is the only way (so far) that we're scoring our guesses.
For this process to really work, we need to apply a more comprehensive scoring system involving (you guessed it) Bigram, Trigram and Quadgram frequencies too. It is not enough that our deciphered message has approximately the same single-letter distribution as English, we want it to have approximately the same Bigram, Trigram and Quadgram frequencies too. So our scoring algorithm ALSO includes scores for these characteristics.
So for example, let's consider our most common bigram in the ciphertext, which is GE (at 5.1%) if our guesses translate this to 'er' (which occurs 2.1% of the time in English) we score this bigram as (5.1-2.1)/(5.1+2.1) = 0.424. To get a total bigram score for this partial decryption key, we add up all the scores for all the other bigrams in the cipher to get a total, which we divide by the score for a completely unassigned key (which equals the number of distinct bigrams in the cipher.).
We do the same for Trigrams and Quadgrams and produce a total score using the sum of squares of the 4 independent measures (Pythagoras would be proud). This ensures that to get a low score you need to make choices that reduce ALL of the measures, not just some of them.
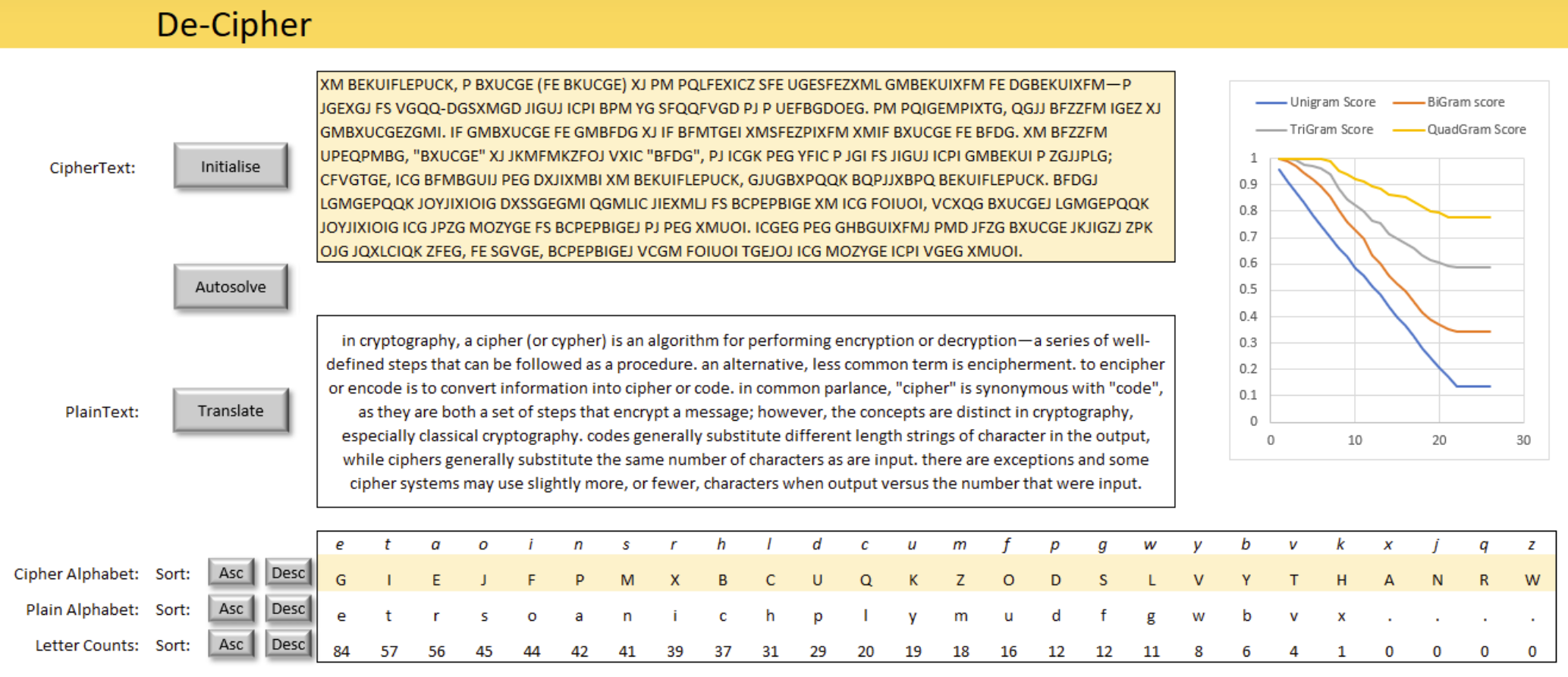
Here are the actual scores after 3 iterations.
Does it work - well yes! and surprisingly well, given that the program doesn't know a single word of English.
It seems that the statistical properties of English are all that's needed to extract sense from (seeming) nonsense, which is rather remarkable.
And the decrypted message is (appropriately) the first two paragraphs from the Wikipedia article about ciphers, the full text of which can be read here... https://en.wikipedia.org/wiki/Cipher