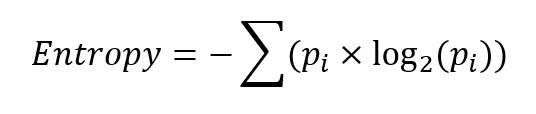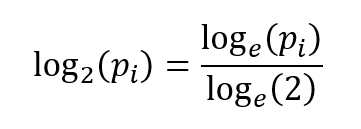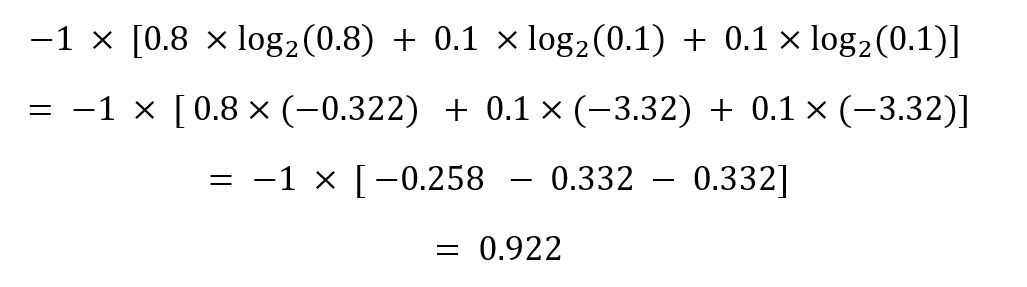In my previous blog, I outlined an approach whereby Excel could provide much interactive support to help break simple substitution ciphers - by counting letter frequencies, by applying guesses, and by highlighting popular bigram, trigram and quadgram patterns and frequencies in your coded message.

But it was still a considerable challenge and a chore, which prompts the question - Can this be solved automatically? Is there some way you can just press a button and have the computer figure out what the plaintext message actually says....?

Let's say this is the message that I'm trying to crack...

Usually, when I have something I want to automate, I work through a few examples, trying to understand my own manual approach well enough that I can abstract some algorithms for solving the problem. But in this case, that didn't seem to help. For sure - I'd start with some guesses about popular letters, I'd look for possible short words in the plain text message, and I'd look at some of those bigram and trigram frequencies - both for feedback about the likelihood that I was on the right track and/or to suggest statistically likely things to try. At some point I would get a gut feeling that I was not on the right track, unwind what I'd done and try something else.

But it was all a bit random and intuitive - not a definite procedure.

How about if I forced myself to be procedural - maybe trying all possible combinations until something works?

Unfortunately, that's completely unrealistic - as there are more than 403 million, million, million, million combinations to try, and then how would I know if something had worked? The computer doesn't understand English and wouldn't be able to tell whether the deciphered text made sense, nor could it develop a gut feeling for whether something was going well.

A common approach to tackling the problem of finding solutions in huge search spaces, is to try to find a way to focus on the most promising-looking options and to ignore the rest. We do this unconsciously all the time - you don't (for example) plan a driving route from A to B by considering driving 100 miles in the wrong direction first, just as much as you wouldn't start solving a cipher by asking - which letter corresponds to q?

So let's start by making a list of all 26 possible guesses for the most popular letter in the cipher (ie. G in this case) and try to assign some score to each in turn, to measure in how good each guess is.

Clearly the letter frequency tables can come to our aid here. We can score our choices by simply comparing the frequency of our chosen letter in the plain text, with what we would expect for normal English. So here we have guessed G = e, and we can see that these letters have a reassuring similarity in their frequency of occurrence.

But we need to score this somehow. I chose to use the absolute difference of these frequencies divided by their sum, which produces a score close to 0 if the numbers are similar, and close to 1 if they are very different. In the example message with G being the most popular letter in the cipher (at 13.3%) guessing the most popular letter in Enqlish e (at 12.5%) produces a score of abs(13.3 - 12.5)/(13.3+12.5) = 0.031 - for that letter alone.

There are 22 separate letters appearing in the above cipher (ie 4 letters are not used). As the other 21 letters in the cipher are not yet assigned a guess, they have a 0% chance of occurring in English, which gives them a score of 1.0. Consider for example the letter I in the cipher which occurs 9.0% of the time, but isn't yet assigned a guess. This has a score of (9-0)/(9+0) which is exactly 1.0.

This is true for all the 21 unassigned letters, so the overall score we would give the entire decryption key at this point is 21+0.031. For normalisation purposes I divide this by the score we would get if no letters were assigned at all (i.e. 22.0) to give 21.031 / 22.0 = 0.956.

So now I have some measure of how good each of the first letter guesses are. The next step is to make the assumption that the correct answer is somewhere in the top 10 scoring letters (remembering that a low score is a good score). So I discard the rest, leaving just the following...

Now I work through each of these entries in the list and create 250 two letter-entries by adding all possible guesses for the second most common letter. I then work through each of these, scoring them, sorting them, and deleting all except the top 10, leaving a result like this one below...

If we continue in this way until the final letter, we might hope to end up with a best-possible decryption key (so long as we didn't accidentally discard it by selecting only the Top 10). And the search is tractable, because our approach ensures that we examine no more than 250 potential decryption keys at each step.

However, and it may be obvious to you already, this process will inevitably pick letters in the order e,t,a,o,i,n because that's the order they appear in Engish letter frequency tables - which is the only way (so far) that we're scoring our guesses.

For this process to really work, we need to apply a more comprehensive scoring system involving (you guessed it) Bigram, Trigram and Quadgram frequencies too. It is not enough that our deciphered message has approximately the same single-letter distribution as English, we want it to have approximately the same Bigram, Trigram and Quadgram frequencies too. So our scoring algorithm ALSO includes scores for these characteristics.

So for example, let's consider our most common bigram in the ciphertext, which is GE (at 5.1%) if our guesses translate this to 'er' (which occurs 2.1% of the time in English) we score this bigram as (5.1-2.1)/(5.1+2.1) = 0.424. To get a total bigram score for this partial decryption key, we add up all the scores for all the other bigrams in the cipher to get a total, which we divide by the score for a completely unassigned key (which equals the number of distinct bigrams in the cipher.).

We do the same for Trigrams and Quadgrams and produce a total score using the sum of squares of the 4 independent measures (Pythagoras would be proud). This ensures that to get a low score you need to make choices that reduce ALL of the measures, not just some of them.

Here are the actual scores after 3 iterations.

Does it work - well yes! and surprisingly well, given that the program doesn't know a single word of English.

It seems that the statistical properties of English are all that's needed to extract sense from (seeming) nonsense, which is rather remarkable.

And the decrypted message is (appropriately) the first two paragraphs from the Wikipedia article about ciphers, the full text of which can be read here... https://en.wikipedia.org/wiki/Cipher

 

I was recently inspired by a Facebook post that shared a number of Spirograph-like images of how 5 of the planets change in distance and direction as seen from the Earth. The original image (used to be) here...

https://luminatress.com/post/184864366539/gaylienz-path-traced-by-these-planets-as-seen

But I was immediately concerned by how 'conveniently symmetrical' those images were and was further troubled by the Mercury image which showed a huge variation in distance from the earth, and a single loop that really didn't seem likely at all. As an amateur astronomer - I have a reasonable intuition for these things.

So I set about creating a simple spreadsheet to produce these patterns for myself, to see if they were valid, and here they are...

---

You may notice that the patterns (as expected) aren't perfectly symmetrical as the ratio of the periods of the planetary orbits are not simple fractional (or integer) multiples of the earth's orbital period (although Venus comes close to 5/8th). You'll also notice Mercury's pattern is very different from the illustration on the astrology website, and I suspect an error on their part. 

How was this done?

The maths isn't too complicated.

First, I looked up the orbital radius and period for each planet from a reputable source (such as: https://nssdc.gsfc.nasa.gov/planetary/factsheet/ and created a look-up table.


I then approximated the planetary orbits as circular and assumed that they all start aligned on the positive X axis on day 1 (which is good enough for this purpose). Given these assumptions we can plot the position of each planet (relative to the sun) at regular intervals using...


Where di is the number of days into the orbit, and Xi and Yi are the X and Y coordinates of where the planet will be.

Written in the style of an excel formula (with names instead of cell references) this looks like...

X=Radius*COS(2*PI()*(Days/Period))

Y=Radius*SIN(2*PI()*(Days/Period))

Two such sets of calculations are needed. One for the position of the planet, and one for the position of the earth on the same day. You *could* produce 8 sets of calculations - one for each planet, but frankly it's simpler and easier just to treat one planet (plus the earth) at a time, and look up (or type in) the orbital parameters you need.

The relative position of the planet from the earth is simply the difference between those two coordinates - ie if we subtract the position of the earth from the position of the planet, that gives us the position relative to the earth.

If we produce a table of such calculations at regular date intervals, we can then plot these relative positions on an X-Y scatter plot, which I've done to produce the above diagrams.

And there we have it.

It probably won't surprise anyone that knows me well, that I quite like puzzles (as/when I have any free time to do them). So when someone recently shared a particularly fiendish logic puzzle with me to solve over Xmas, I happily sat down with a couple of mince pies and a glass of mulled wine one evening to give it a go.

As logic puzzles go, this one was satisfyingly difficult (thanks "Puzzle Baron", whoever you are). It was bigger than usual, there were no giveaway clues (the kind that allow you to put a tick in the box straight away) and several clues were couched in terms of either statement A is true (or statement B is) that are difficult to do much with at first...

---

But I gave it a go anyway, steadily worked my way through all the clues, and after about an hour had almost reached the end, when I discovered a contradiction. Somewhere along the way, I must have made a mistake, probably in carrying out all the routine admin of updating all the affected cells in the grid. So I started over, but frustratingly, the same thing happened again, but this time with a different contradiction.

It was at this point that I asked myself - surely there's a better way to do this with an Excel spreadsheet (automated of course). I didn't exactly want to press a button to solve the puzzle automatically (where's the fun in that?) but I did feel that I wanted some kind of "power tool" to help me with all the routine updates to the grid, and to do them without any mistakes!

And so I wrote my logic puzzle "power tool", which I describe below. Now as I don't have (and won't presume) Puzzle Baron's permission to share their puzzle with you, I've illustrated the tool with excerpts from that old favourite logic puzzle "Who owns the Zebra" - which even has its own Wikipedia entry, in case you fancy giving it a try.

So here's how I did this.

First I created a table of categories and values....

I then wrote software to automatically produce a puzzle-solving grid from the above, with a restart button to run the code anytime I wanted to start over.

 

Each cell in the grid was set up to ONLY accept T (True), F (False) or a number, so if you wanted to (say) record the fact that House #2 has a red door, then you just right-click the appropriate cell, and select True from the drop-down picklist. The value entered is then colour-coded (in green or red) using conditional formatting to provide good visual feedback. 

Why do we need a number? Well that's so you can record the number of the clue which tells you something about that cell, even when you can't yet write TRUE or FALSE there. For example, if clue #2 tells you that EITHER house #1 has a yellow door OR house#5 has a blue door, then you can write it like so...

...and when either one of those 2's disappears as a consequence of other logical steps, you can immediately see that clue #2 is now ready to be acted upon.

So far so good. We have an electronic means of drawing a grid and interacting with it, but solving the puzzle is still an entirely manual task and I wanted a power tool (which is where it gets interesting).

Note that it's possible to write code that is executed when something changes on the sheet, so we can use this to execute code which automatically writes FALSE into the rows and columns, whenever you mark a cell as TRUE. So here, when I declare that house #2 has a red door, the tool automatically excludes house #2 from having any other door colour and excludes any other house from having a red door...

And of course, given that the grid has a diagonal symmetry, how about if we automatically reflect everything about the diagonal while we're about it.

In words, this just means that if house #2 has a red door, then the house with a red door, is house #2. 

But this diagonal symmetry means that everything down the diagonal will be true - (ie, house #2 is house #2), so all grids (in practice) start with the diagonal pre-populated as true...

And the automated actions we've already described, add all those FALSE entries automatically before we even start...

As Sherlock Holmes once said... “When you have eliminated the impossible, whatever remains, however improbable, must be the truth.”

When comes to logic puzzles, that means automatically recognising when only one possibility exists, and setting it to TRUE, for example this...

...is turned into this...

And finally, we should recognise that once we know (for example) that House #3 has an Ivory Door, then anything ELSE we know or learn about House #3 will also be true for the Ivory Door (and vice versa). So for example, if we learn that the Norwegian DOESN'T live at house #3, then he doesn't have an ivory door either!

So the grid above automatically becomes the grid below.

 

These simple rules, once automated, and run in reaction to any changes you make the grid, take away the mundanity of solving logic puzzles. Of course for some people, I appreciate that's what interests them, but for me, finding ways to automate tedious repetitive actions, and leaving the thinking parts is what I do.

Did it help? Absolutely. Using this tool, I solved the original puzzle I was given at Xmas in about 10-15 minutes, whereas without it I twice spent an hour only to be floored by an admin mistake. For me - that's a worthwhile achievement - and one worthy of another glass of mulled wine.

---

A final footnote - in case anyone with sufficiently advanced Excel skills wishes to try this for themselves here are some important tips...

As each change automatically produces many more changes, it's important not to automatically update anything which already has the desired value (else the cascade of changes will never finish). It's also sensible to check that you're never changing a TRUE value to a FALSE one (or vice versa). Not only is that the signal for a contradiction (which you should flag to the user) it will likely produce an infinite loop of changes.

On a large puzzle, the cascade of changes can cause Excel to recurse very deeply. It's entirely possible that Excel runs out of stack memory before coming up for air! So in an improved version of the code, I ensured that it didn't apply updates immediately, but instead built up a "to-do" list of changes each time I typed something. A separate routine then carried out these actions a few seconds later and serially one after the other, until there was nothing left to change. This doesn't run out of stack memory and works like a charm. :) 

Solving Wordle with Excel

If you're reading this, I assume that you're already familiar with the new online word game Wordle, which was invented by Josh Wardle, and is currently (April 2022) owned and published by the New York Times.

In this game, you have 6 chances to guess a secret 5-letter word, and you get feedback on each guess to help you narrow down your search. I thought it would be fun to build an Excel workbook that can play the game and solve Wordle puzzles automatically.

Design and Data Entry

The first task was to fashion a reasonable look-a-like representation of the grid…

This is built as two Excel tables (the column headers are in a hidden row), the left one to enter letters, and the right one to enter marks.

Each table uses data validation to control what can be entered. The letter table uses an A-Z picklist, and the marking table allows entry of 0, 1, or 2 to indicate the appropriate mark (0=grey, 1=yellow, 2=green). Conditional formatting is used to colour the cell backgrounds according to this number in the marking table (using the same palette as the NYT website) and by making the font colour the same as the background colour, you can’t see the numbers.

Now if our software is going to guess words, it needs to know all the admissible words. It turns out that there are only 2309 of these, and a quick Google search will quickly find a full list. Here’s one place I saw them… https://www.wordunscrambler.net/word-list/wordle-word-list.

I downloaded such a list and put all of the words into a table.

Marking an Answer

The next task is to be able to mark a guess against a secret word. This will need to be written in software. Whilst it may not be obvious yet, if you’re going to be able to judge whether a guess is a good one, you need to be able to ‘test mark’ it against candidate secret words, so let’s consider how to do this.

As you’ll probably know, green is awarded for a correct letter in the right place, and yellow for a correct letter in the wrong place. But there are subtleties – if your guess contains double letters and the secret word contains only one, you’ll only get the ‘better scoring’ one marked. And if the secret word contains a double letter but your guess contains just one, then again you get the better scoring mark.

The way I approached this was to consider that one mark is potentially available from each letter of the secret word, and given to at most one place in the guess. So I loop over each secret letter. If the guess has the same letter in the same place – it gets a green. If (and only if) it doesn’t, then I search the other letters of the guess to see if I can give away one yellow, but ONLY if it isn’t already green (by some other route).

Making a Guess

This is the hard part (of course!).

Let’s consider that we’re part-way through a game. The first thing we do is identify all secret words that are still possible. To do this, we create a list of all 2309 wordle words from our list and mark all the guesses so far against each of these. If it matches the markings so far, we keep it, if not, we remove it from the list.

Now we have a list of candidate secret words. Picking the next guess at random from this list of candidates might work, but it’s not the best possible strategy. A good player will want to squeeze as much information as possible out of every turn. How do we do that exactly?

Well, one approach is to mark every possible guess against each candidate solution in turn and count how many times each possible score comes back. That sounds like a lot of work, but it only takes a few seconds in software if you do it efficiently.

For example, let’s say after 2 guesses, we have this position.

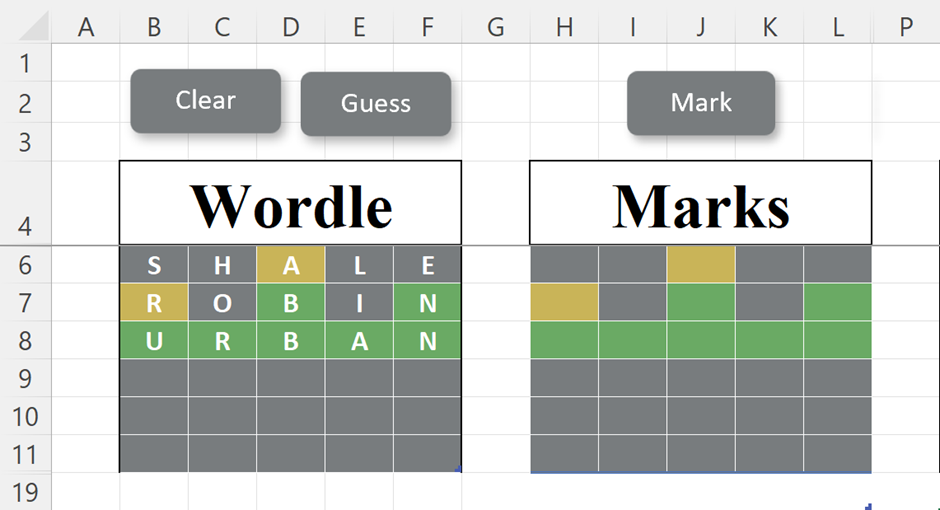
It turns out that there are only 10 possible candidate solutions that it could be…

BILLY, DILLY, DIMLY, FILLY, FILMY, HILLY, IDYLL, IMPLY, MILKY, WILLY

If we were to try an example guess ABACK against each of these possibilities, we’d get a distribution of marks that looks like this…

Mark Distribution for ABACK

8/10 (80%) of these words have no letters in common, and would return 5 grey squares, MILKY would award 1 yellow square for the letter K, and BILLY would award 1 yellow square for the letter B.

So 20% of the time (i.e. if the secret word was MILKY or BILLY) we’d have only one possible candidate left after guessing ABACK, but 80% of the time we’d still be left with 8 candidates, which isn’t much of an improvement from the 10 we had before, so most of the time, ABACK wouldn’t be a great guess at this point.

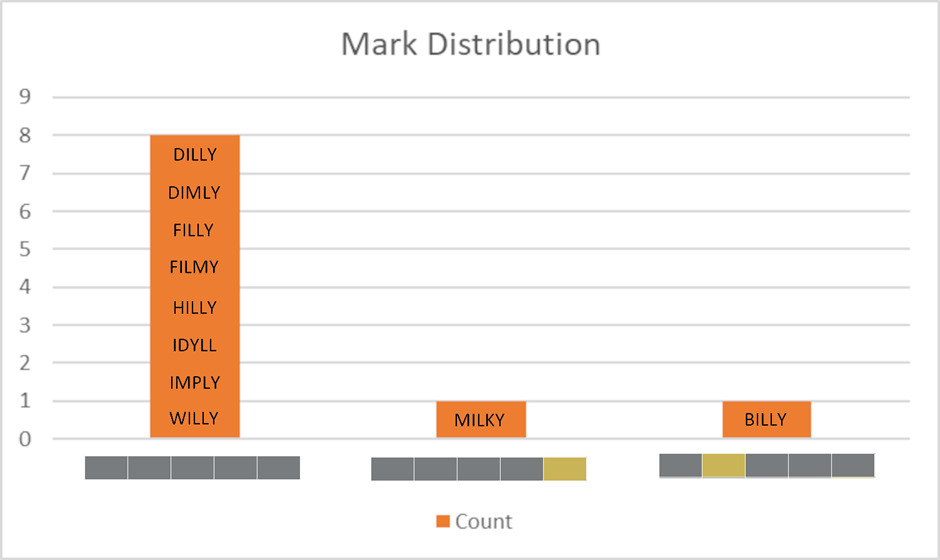
Hopefully, it will be clear that it’s much more useful if we can find a guess that spreads the marks out more - ideally if we can find a guess that would give a different mark for each of the remaining candidates…

An "Ideal" Mark Distribution

Such a guess would guarantee that whatever response we get, we are GUARANTEED to know what the right answer is next time, as whatever the score, it relates to just one possible candidate word.

Unfortunately, in this situation (and most of the time) no such word exists, so we need to pick the best answer from the available choices. It turns out that EMBED is a good guess, as it produces the following distribution of marks.

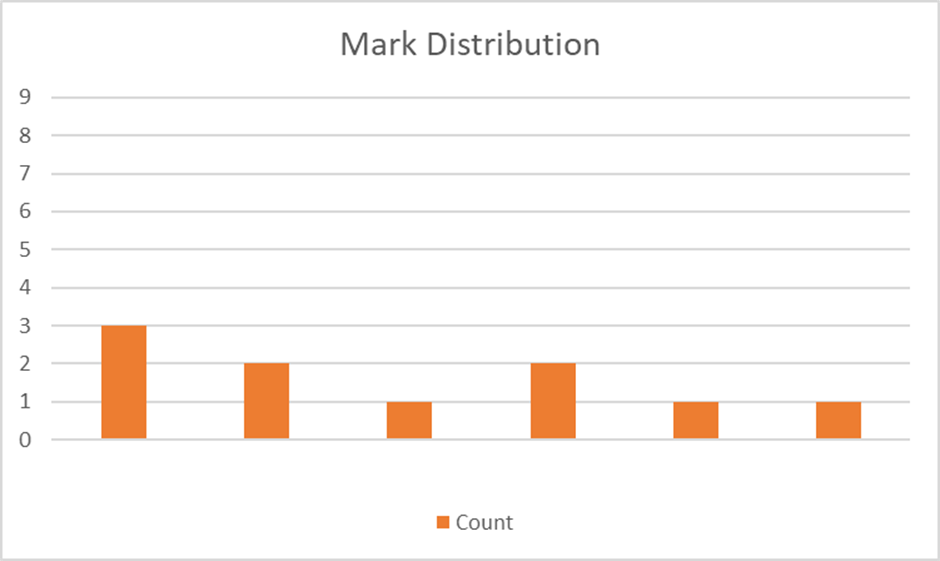
Mark Distribution for EMBED

Here, 30% of the time we will get a unique answer, 40% of the time we will have a choice of 2, and 30% of the time we will have a choice of 3. So the best case happens 30% of the time, and even in the worst case, we’re only left with 3 to pick from. EMBED is clearly a much better guess than ABACK.

How did we find EMBED? Well, it’s the choice with the shortest, tallest bar of all the possible wordle guesses. Put another way, I’ve scored each and every one of the possible guesses (all 2309) using the height of their tallest bar (e.g. 3 for EMBED, and 8 for ABACK) and I’ve picked a guess that has the lowest score. It’s the least worst-case option. Yes, there are probably lots of guesses that are just as good as EMBED. It's not likely to be unique.

If you’re interested, this approach was described in a recent Numberphile video on Youtube, using the game of MasterMind as a simpler example. https://www.youtube.com/watch?v=FR_71HyBytE

Another Approach

It’s not the only way to choose a solution. Statisticians and data scientists might describe these distributions more precisely in terms of their Entropy. Entropy is (sort of) a measure of how random or likely something is.

The distribution we saw under ABACK with 8 of the answers having the same mark (out of more than 200 possible marks) seems pretty unlikely to arise by random chance, so it’s known as a low entropy arrangement. Whereas finding an arrangement where the answers are more evenly spread across lots of different values would seem to be a more likely situation – so EMBED has a higher entropy distribution than ABACK.

There’s a formula to calculate this of course, it’s…

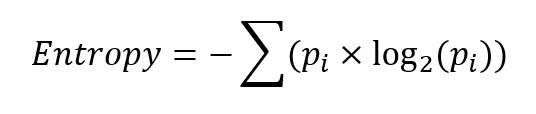
Where p_i  is the probability of each outcome, and Σ means adding up all the terms within the brackets.

Note that VBA doesn’t have a log (base 2) function, it only offers natural logarithms. But it's simple to convert from a logarithm to another base, as the base change rule is…

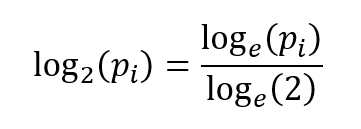
log_e(2) is a constant (0.693), so to calculate we just need to divide by 0.693. But as we only want to know which word has the largest entropy, this isn’t absolutely necessary, and you could get away with natural logs if you prefer.

In the case of ABACK then, we have an 80% chance of the first option, a 10% chance of the second, and a 10% chance of the third, so the entropy is…

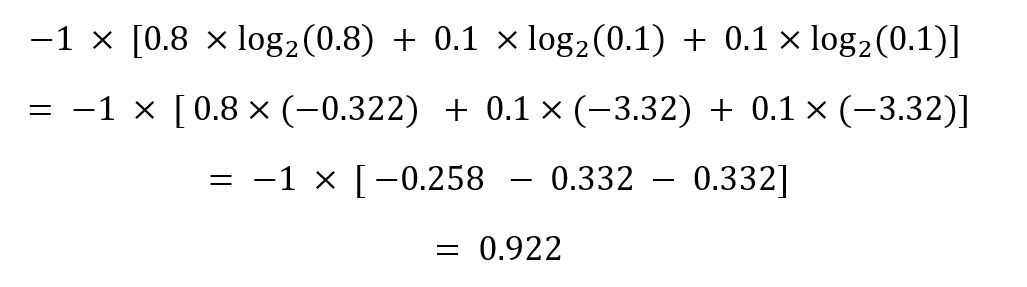
Whereas with EMBED, the entropy calculated by the same formula is 2.45 – indicating a more randomly spread, and therefore more desirable guess. In this application, we want to pick the highest entropy guess.

In practice, the highest entropy choice of all 2309 words is FIELD with an entropy of 2.65. If we examine the distribution of marks we get with FIELD we can see that they’re now spread over 7 different values and that 50% of the time we would get a unique answer. This is even better than we achieved with EMBED, even though both EMBED and FIELD have the same height tallest column.

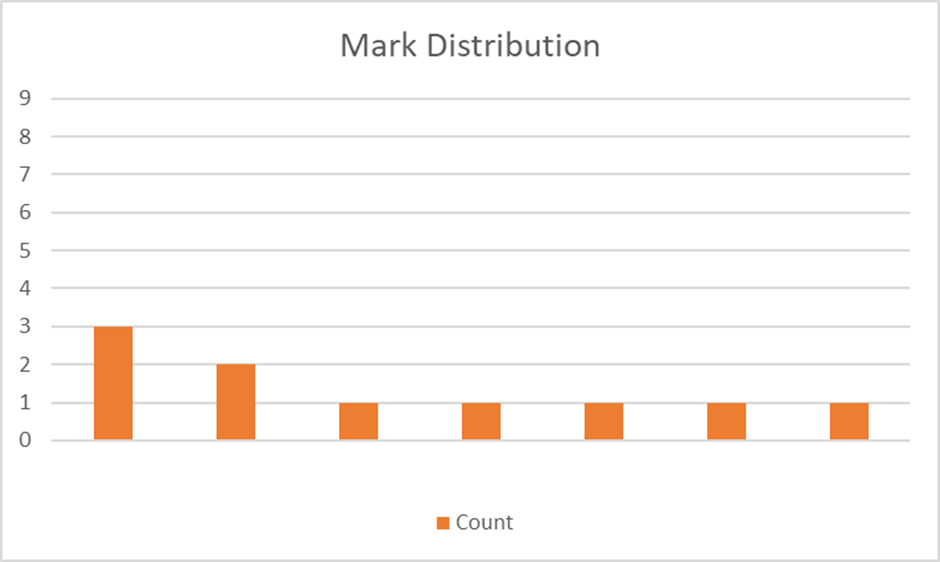
Mark Distribution for FIELD

So it can be seen that entropy makes more discriminating choices (that should be slightly better), at the expense of a more complicated evaluation function. But in practice, the improvement (measured in how many steps it takes to solve random Wordle puzzles) is very small at best. In trials of about 1000 runs this algorithm (with a step or two yet to be described) averages about 3.65 guesses with the first algorithm and about 3.55 guesses with entropy. It’s a difference of only 2%.

This approach is described further in a 3Brown1Blue video on Youtube: https://www.youtube.com/watch?v=v68zYyaEmEA

Making the final guess

Thus far, I have only described how to choose guesses that efficiently reduce the number of candidate solutions. If this is all you do, you won’t actually solve the puzzle, you’ll just get stuck in an endless cycle of making equally bland and ineffective guesses that fail to reduce the number of candidates to less than 1.

There comes a time when it’s necessary to bite the bullet and actually guess the answer from one of the candidates. Here are my thoughts about when to do that:

• When there’s only 1 candidate solution left.
  1. It’s REQUIRED to guess this solution at this time. This is a ‘no brainer’

• When there are only 2 candidate solutions left.
  1. A random guess from these gives you a 50% chance of being right the first time, and a guarantee of being right the second time, so on average it will take 1.5 turns. But if you try one more reduction step, then it will always take 2 turns.
  2. So it’s better to make a random guess when you have just 2 candidates

• When there are only 3 candidate solutions left.
  1. A random guess of a candidate gives you a 1/3 chance of being right each time you try. On average it will take 2 turns, or fewer if there’s a candidate that itself scores (1,1,1).
  2. If your best scoring non-candidate is (1,1,1) (this is quite likely) it will take 2 turns if you reduce one more time, but if your best scoring option is only (2,1) it will take an average of 2.33 turns.
  3. So a simple rule here might be to always pick the best scoring candidate – on average this is at least as good as any other strategy. However, if you’re on your 5^th turn, you might prefer the certainty of taking that (1,1,1) option. But if you’re on your 6^th turn you might prefer to take the 1/3 chance you might get it right, rather than the certainty of failure. It’s complicated and context-sensitive.

• I’ve not analysed the situation with 4 or more candidates, but it’s only going to get more complicated. So I’m simply going to assume that if the case with 3 candidates is marginal, then with 4 candidates any benefit of making a guess from the candidates will mostly be lost. So in my code, if I have 4 or more candidates - I reduce, unless I’m on my last guess.

Here’s a very quick and easy way of implementing the above strategy. If you have 3 candidates or fewer (or you are on your last guess) only pick guesses from the candidates, not the whole set of 2309 wordle words.

Performance Optimisations

Marking and scoring 2309 words against a shortlist of candidates during the mid-game isn’t too onerous, but for the first and second guesses, it does take tens of seconds. Here I can recommend two important optimizations.

The first guess is always from the same “no information” starting point. So it makes sense to score all 2309 words just once and to store all the scores (for future reference) along with each word. You could then ALWAYS start with the best word if you really wanted to, but that’s not very interesting. A more varied approach would be to pick something at random from the top 5% or 10% best-scoring words.

The second guess typically also has a lot of candidates to look at. But you’re still just narrowing down the possibilities, you don’t need to examine all possible guesses. It would be astonishing if you can’t find an excellent choice amongst (say) 250 examples that wouldn’t be 99% as good as searching through the whole set of 2309. So yes, in the second round, I only examine 10% of all possible guesses. I only look at the full set from the 3^rd round.

Thirdly, when dealing with markings, and comparing to see whether a test word matches the mark of a marked word, it’s not efficient to compare each cell in turn. Instead, I store and compare the marks as a 5 digit ternary (base 3) number. So instead of 5 comparisons, I perform one.

And finally, a surprising effect of the 3 candidates or fewer trick to pick a guess from the candidates, rather than from the whole dictionary, made much more difference to the speed of execution than it did for the average number of guesses. In practice, instead of taking about 5 seconds to solve a game, it takes about 2.5 seconds.

Going for Broke

The success of Wordle has inspired some 'more difficult' variants on the theme.

Quordle https://www.quordle.com where the goal is to solve 4 puzzles at once in 8 turns.
Octordle https://octordle.com/ where the goal is to solve 8 puzzles at once in 13 turns
and even Absurdle https://qntm.org/absurdle which is Wordle, with the secret word changing dynamically as you play, trying to cut you as little slack as possible.

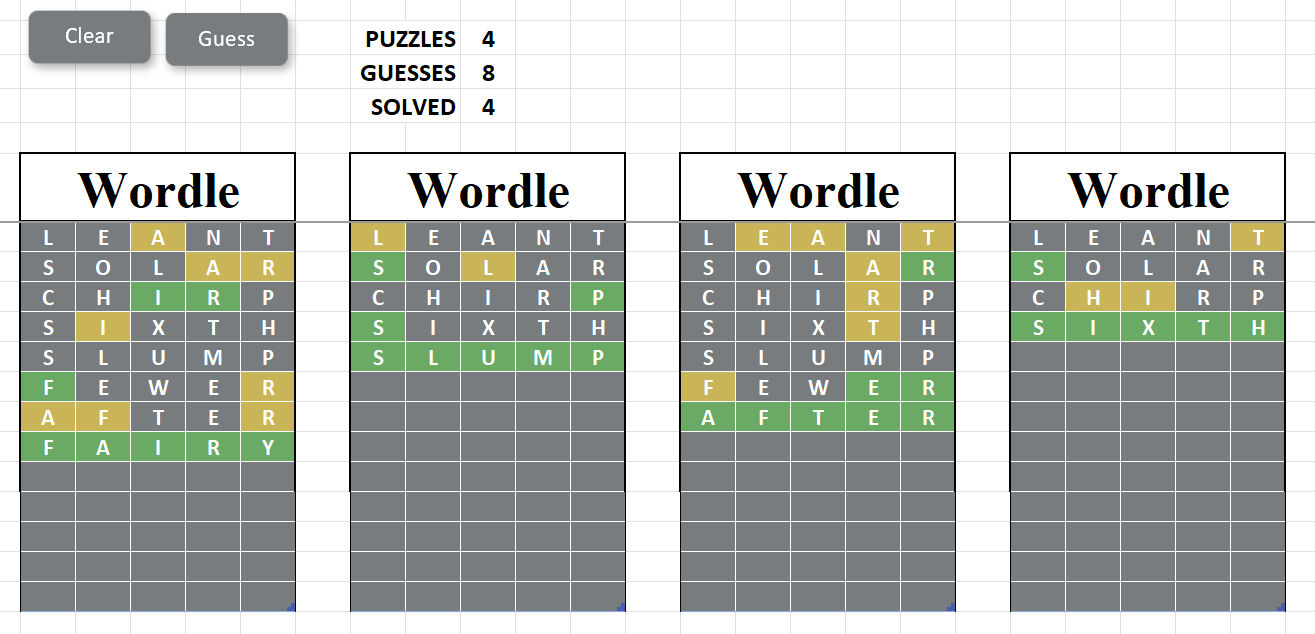
It's perfectly possible to extend the Excel workbook and the code to an 8 puzzle variant, and here it is (with marking tables hidden)

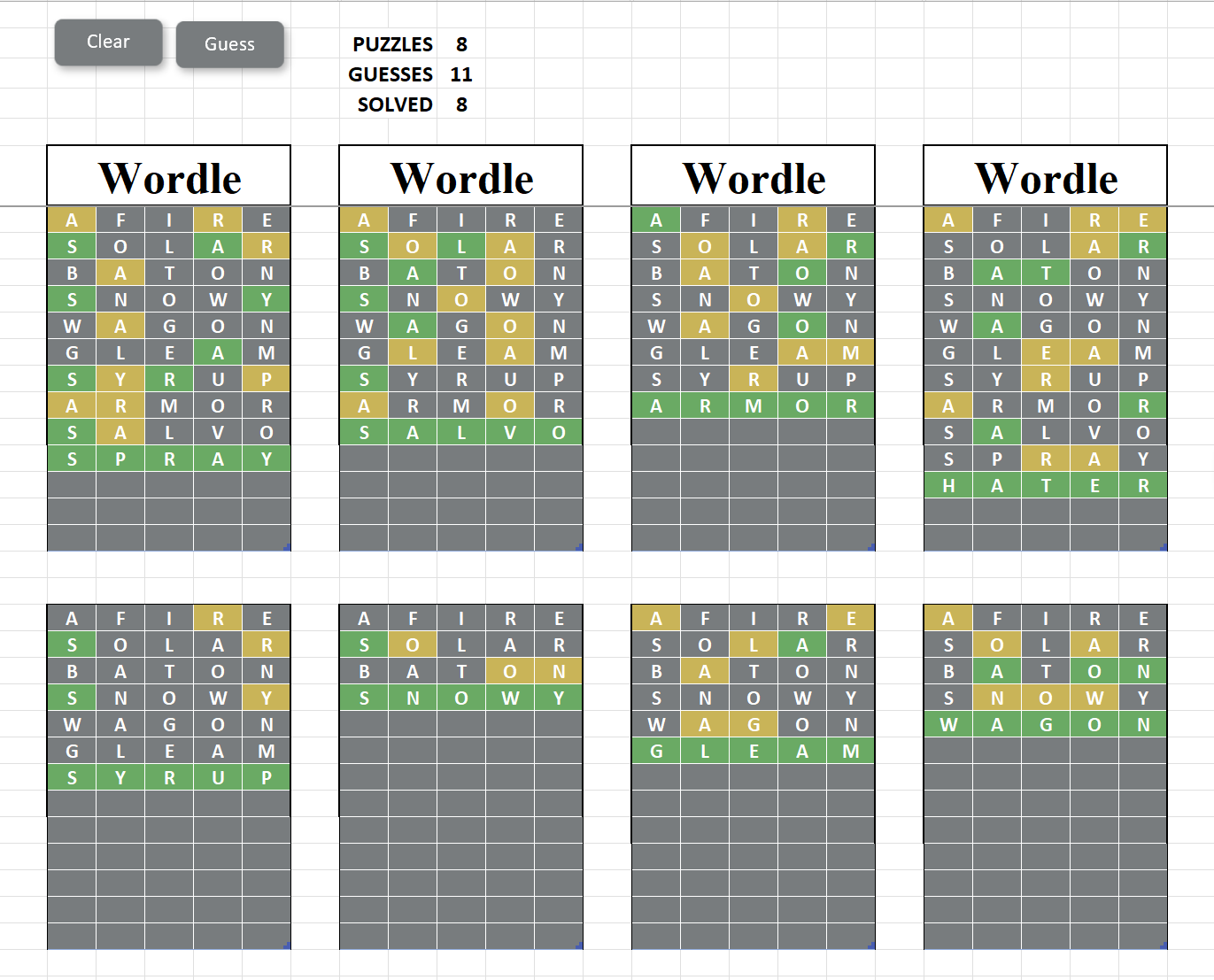
Extension of Wordle solver to crack up to 8 puzzles at once

Apart from the obvious need to work with 1, 4 or 8 tables (as selected by the PUZZLES value) the extensions to the algorithm are not all that major.

The Making a Guess routine produces a single, merged list of all candidate solutions for all puzzles before searching for the largest entropy guess that would distribute them (as before). The logic that argued when to cut over to guessing the answer rather than reducing the candidates is applied only to this merged list (as it's only really justified when solving the final puzzle) so an additional check is made that if (at any time) there is only one candidate left for a puzzle then that candidate IS the next guess, ignoring everything else.

The typical performance of this algorithm is about 11 to 11.5 guesses to solve the whole puzzle, taking about 30 seconds a time.

-oOo-